Principal Component Analysis (PCA) is a fundamental tool in machine learning and data analysis. We propose a distributed PCA framework that enables multiple workers to compute distinct eigenvectors simultaneously using a novel Parallel Deflation Algorithm. Our method allows for asynchronous updates while maintaining provable convergence, addressing a key theoretical gap in model-parallel distributed PCA. We demonstrate that our approach achieves comparable performance to EigenGame-\(\mu\), the state-of-the-art PCA solver, while providing stronger theoretical guarantees.

PCA is widely used in dimensionality reduction and feature extraction. Traditional centralized approaches struggle with scalability in large datasets, necessitating distributed methods. Model-parallel PCA algorithms, such as EigenGame, have demonstrated success in distributing computations across multiple workers, but they rely on strict sequential dependencies.

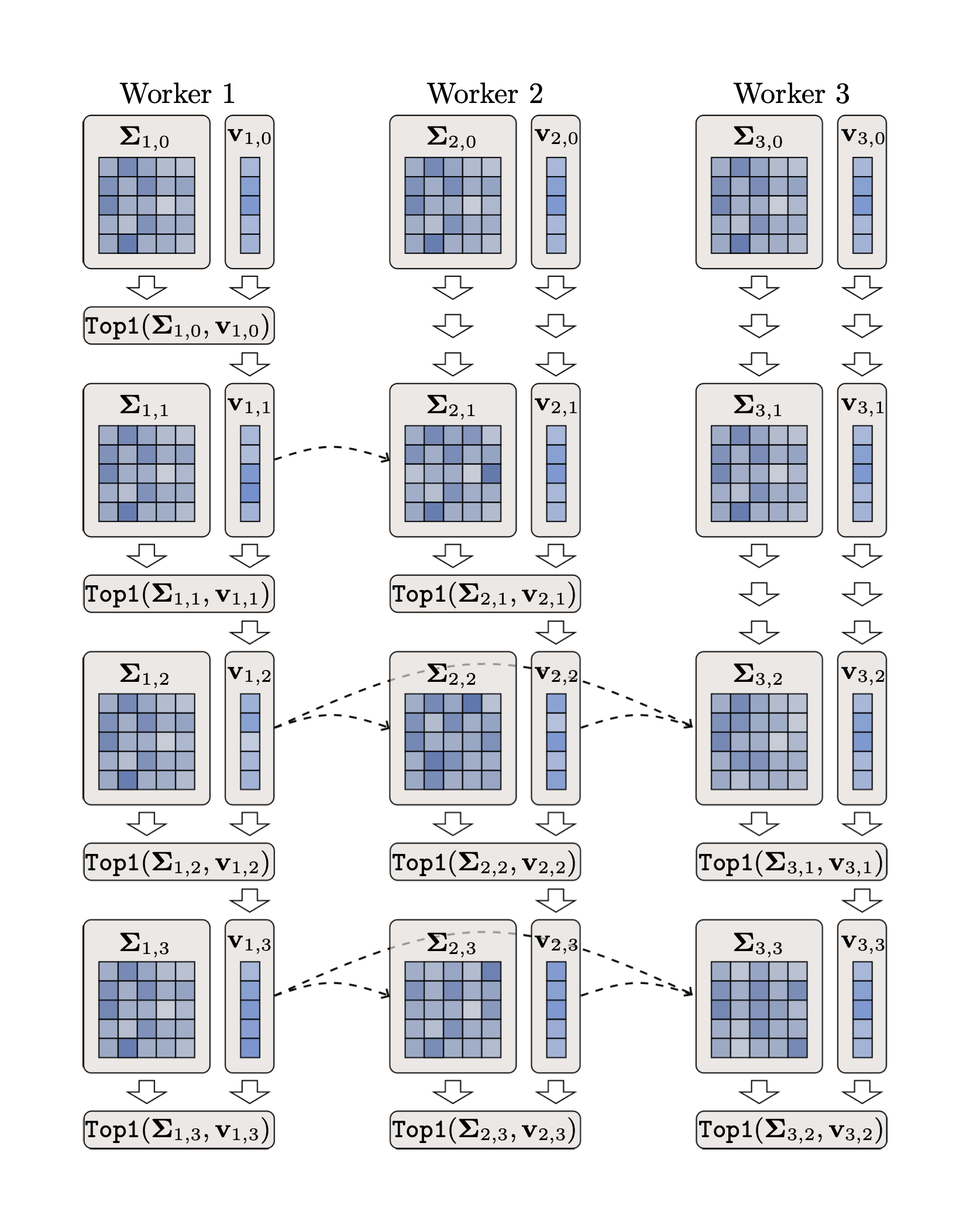
We introduce Parallel Deflation, a model-parallel PCA approach that breaks the strict dependencies of previous methods, allowing multiple workers to refine their eigenvector estimates asynchronously. Our theoretical analysis provides provable convergence guarantees, a missing piece in prior model-parallel approaches.

Several approaches have been explored for distributed PCA:

• Eigenvector-based methods: Classical PCA relies on matrix decomposition techniques such as QR decomposition and Lanczos methods, which do not scale efficiently to distributed settings.
• Stochastic optimization: Methods like Oja's rule and stochastic gradient approaches offer scalable alternatives but lack strong theoretical guarantees in distributed settings.
• Data-parallel PCA: Existing distributed PCA frameworks partition data across workers but require centralized coordination, limiting efficiency.
• Model-parallel PCA (EigenGame): Recent approaches model PCA as a game where workers compute individual components. However, existing methods require strict sequential dependencies and lack theoretical analysis.

Our work advances model-parallel PCA by removing strict sequential dependencies and providing provable convergence results.

We focus on computing the top-\(K\) eigenvectors of an empirical covariance matrix \(\Sigma\). Given a dataset \(Y\) with \(n\) samples and \(d\) features, the covariance matrix is given by: \(\Sigma = Y^\top Y\). The goal is to find the top-\(K\) eigenvectors of \(\Sigma\) efficiently in a distributed setting, without requiring strict sequential dependencies.

Our algorithm distributes the computation of \(K\) principal components across \(K\) workers. Unlike traditional deflation methods that require sequential eigenvector computation, we introduce a parallel iterative approach:

• Initialization: Each worker starts with a rough estimate of its assigned eigenvector.
• Parallel Updates: Workers refine their estimates iteratively, incorporating updates from other workers.
• Deflation: The covariance matrix is deflated iteratively using the best available eigenvector approximations.

We provide theoretical guarantees for the convergence of the Parallel Deflation Algorithm. Our analysis shows that:

• Global Convergence: The algorithm converges to the true eigenvectors under mild assumptions.
• Asynchronous Updates: The approach remains stable even when workers update asynchronously.
• Error Bounds: We derive tight error bounds, demonstrating that convergence accelerates as updates propagate.

These results establish a strong theoretical foundation for model-parallel PCA, addressing a key gap in prior work.

We compare Parallel Deflation against EigenGame-\(\alpha\) and EigenGame-\(\mu\) on synthetic datasets and real-world benchmarks such as MNIST and ImageNet.

• Speed: Our method achieves faster convergence than EigenGame-\(\alpha\) while matching EigenGame-\(\mu\).
• Scalability: Our approach scales efficiently to large datasets without requiring strict dependencies.
• Accuracy: Achieves comparable reconstruction error to EigenGame-\(\mu\) while offering theoretical guarantees.

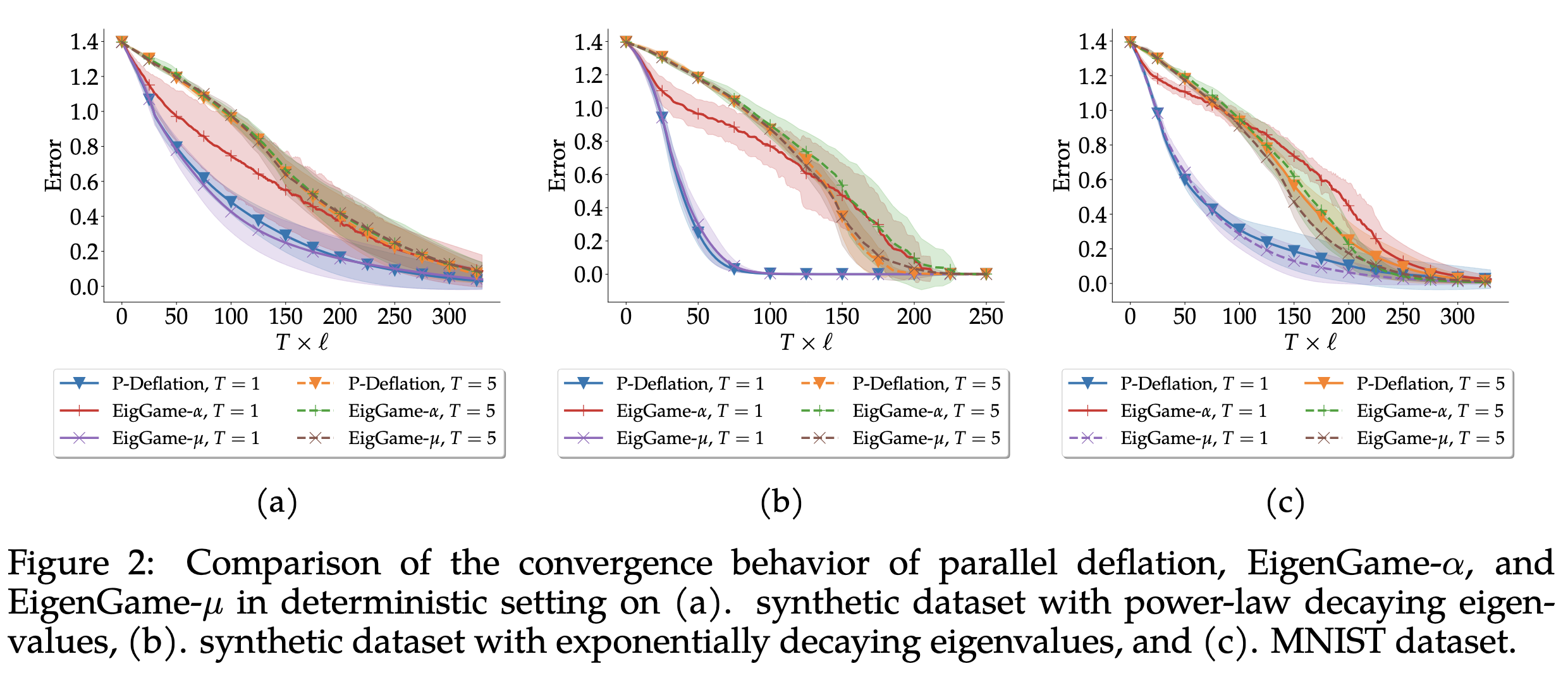
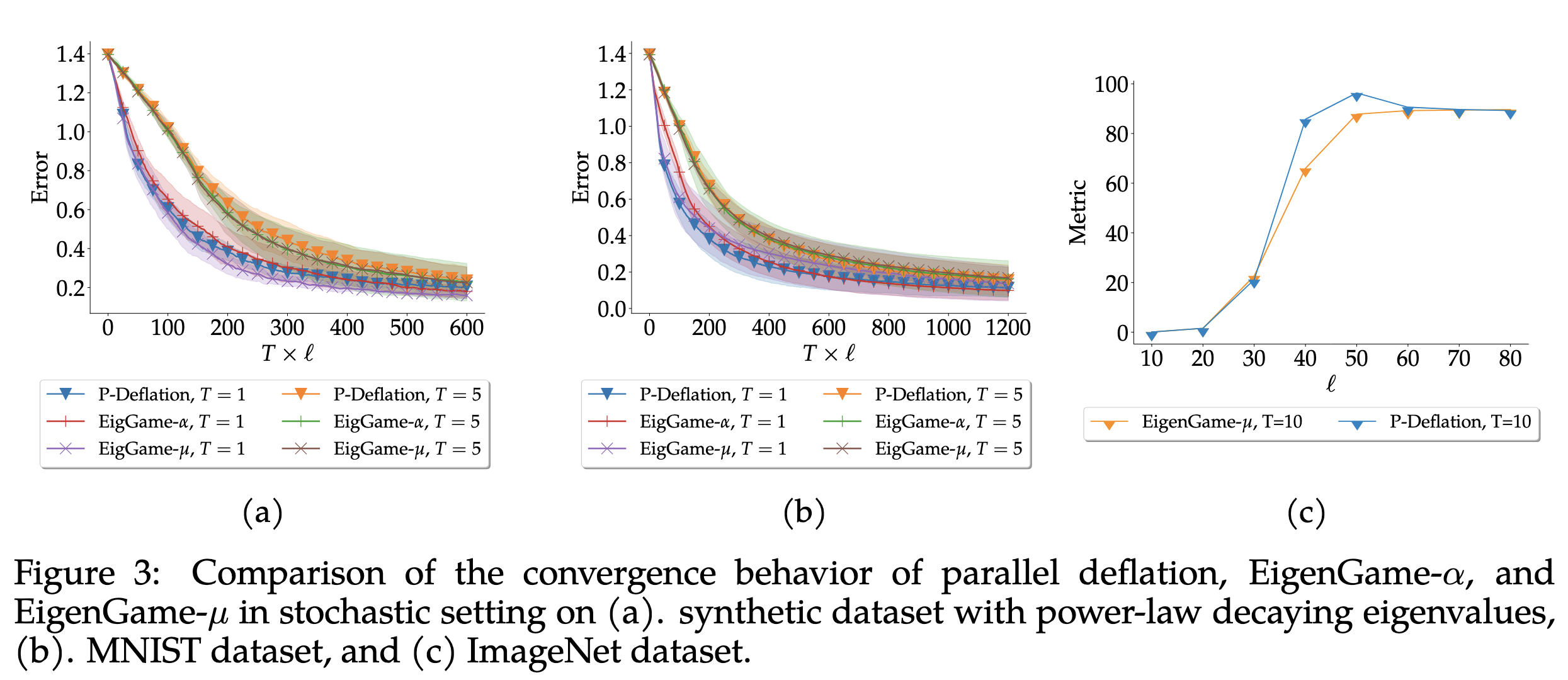
We present Parallel Deflation, a novel model-parallel PCA framework that removes sequential dependencies and provides provable convergence guarantees. Future work includes:

• Extending the method to other eigenvalue problems.
• Exploring adaptive update strategies for further efficiency.
• Applying the approach to large-scale deep learning models.