
|
|
|
|
|
|
|
Code [GitHub] |
Paper [arXiv] |

Solving systems of linear equations is a cornerstone of computational science but becomes exceedingly challenging as the dimensionality increases. Quantum algorithms have shown promise in tackling this problem efficiently, offering exponential speedups over classical methods. However, these quantum advantages are often constrained by the condition number of the matrix in question. In our recent paper, we propose a novel quantum algorithm inspired by the classical proximal point algorithm (PPA). This meta-algorithm enhances existing quantum linear system solvers by improving their dependence on the condition number, thereby broadening their applicability to more ill-conditioned problems. By carefully selecting a parameter \(\eta\), our method effectively preconditions the linear system, mitigating the bottleneck imposed by large condition numbers.
Solving systems of linear equations is essential in numerous applications, from scientific computing to machine learning. Classical algorithms like Gaussian elimination and iterative methods scale poorly with the problem size, often rendering large-scale problems intractable. Quantum algorithms offer a potential breakthrough by reducing the dependency on problem dimensions from polynomial to logarithmic, as demonstrated by the Harrow-Hassidim-Lloyd (HHL) algorithm. Despite this, the performance of quantum algorithms is severely impacted by the condition number \(\kappa\) of the matrix, which measures the sensitivity of the system to numerical errors. High-condition numbers can significantly degrade the efficiency of quantum solutions, a challenge we address in this study.
Our approach leverages the classical proximal point algorithm (PPA), a method renowned for improving problem conditioning in optimization tasks. By adapting PPA to the quantum domain, we introduce a framework that enhances the performance of existing quantum linear system solvers. The key innovation lies in modifying the matrix to be inverted, thus reducing the effective condition number and improving convergence rates. This method can be seamlessly integrated with various quantum solvers, providing a versatile tool for tackling a broader class of linear system problems.
The Quantum Linear System Problem (QLSP) aims to prepare a quantum state proportional to the solution vector \(x^\star\) of a linear system \(Ax = b\). This task is central to many quantum algorithms, including those for solving differential equations, machine learning, and optimization problems. Existing quantum algorithms, such as the HHL algorithm, achieve significant speedups over classical methods by reducing the complexity from polynomial to logarithmic in the problem dimension \(N\). However, their performance is often limited by the condition number \(\kappa\) of the matrix \(A\).
The condition number \(\kappa\) is defined as the ratio of the largest to the smallest singular value of \(A\). High-condition numbers indicate ill-conditioned systems that are susceptible to numerical errors, which can significantly slow down convergence and reduce accuracy. Addressing this limitation is crucial for extending the applicability of quantum algorithms to real-world problems, which often involve ill-conditioned matrices.
A proper definition of the QLSP problem is as follows:

We present a novel meta-algorithmic framework that enhances the performance of existing quantum linear system solvers. Our contributions are as follows:
Our approach stands out by directly approximating the solution vector \(x^\star = A^{-1}b\) through iterative refinement. This is in contrast to existing methods that focus on approximating the inverse of the coefficient matrix \(A\). By inverting a modified matrix \((I + \eta A)\), our algorithm effectively preconditions the system, resulting in a better-conditioned problem that converges more rapidly.
Our proposed algorithm employs the proximal point algorithm (PPA) to iteratively solve the QLSP. The core idea is to invert the modified matrix \((I + \eta A)\) instead of the original matrix \(A\), thus improving the system's conditioning. The algorithm proceeds as follows:

The convergence rate and error bounds of our algorithm are rigorously analyzed. By carefully choosing the parameter \(\eta\), the algorithm balances the trade-off between runtime and approximation error. Our theoretical analysis demonstrates that the proposed method achieves faster convergence and greater accuracy than existing quantum solvers, especially for ill-conditioned problems.
We also provide a detailed complexity analysis, showing that our method significantly reduces the dependence on the condition number \(\kappa\). Please check our paper for a complete and detailed theoretical analysis.
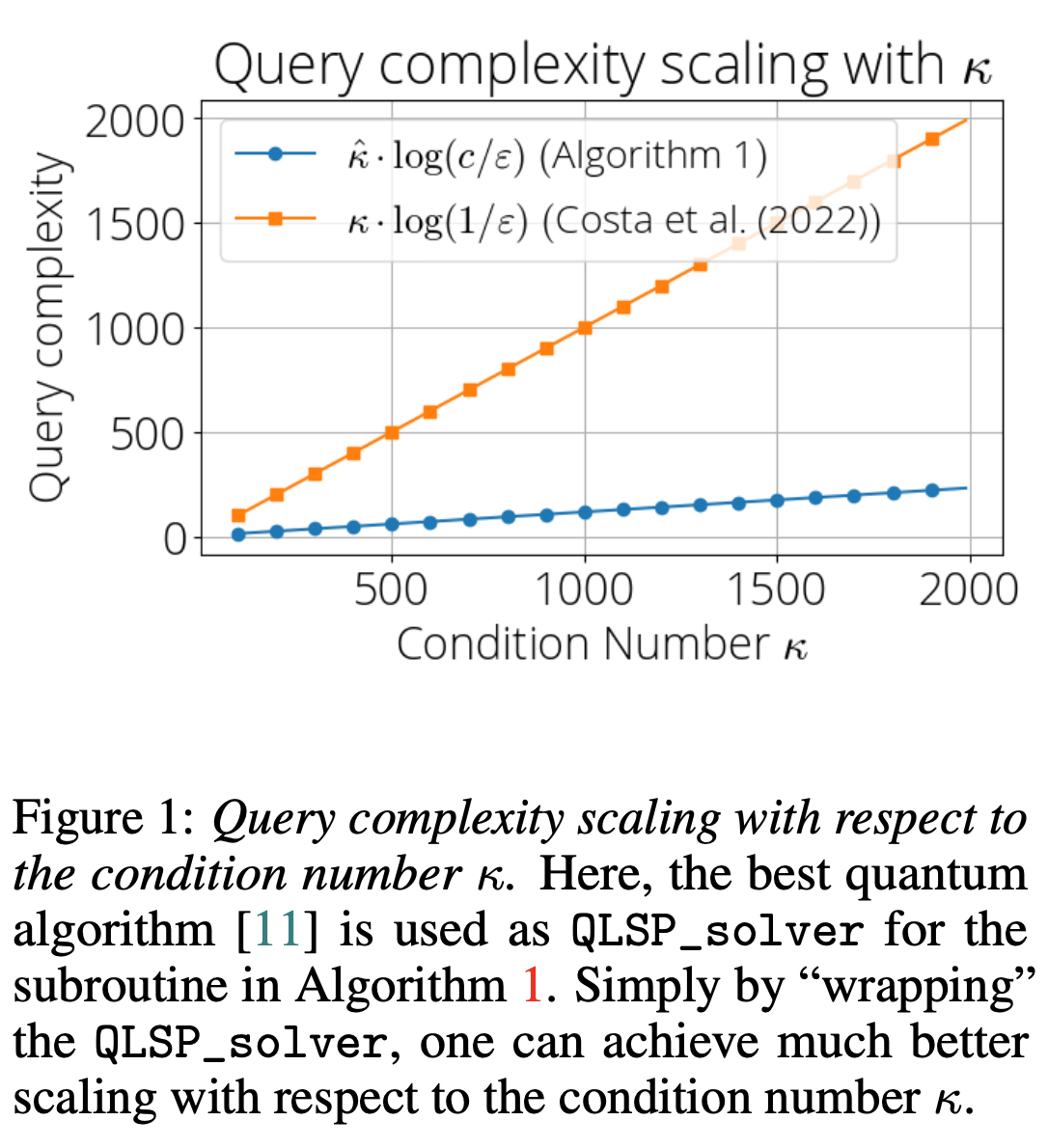
In Figure 1, we show how the query complexity scales as a function of the condition number \(\kappa$\). The orange line is the state-of-the-art QLSP solver based on the discrete adiabatic theorem. Simply by “wrapping” the original QLSP solver with our proposed method, the query complexity to achieve a fixed accuracy improves as \(\kappa\) increases.
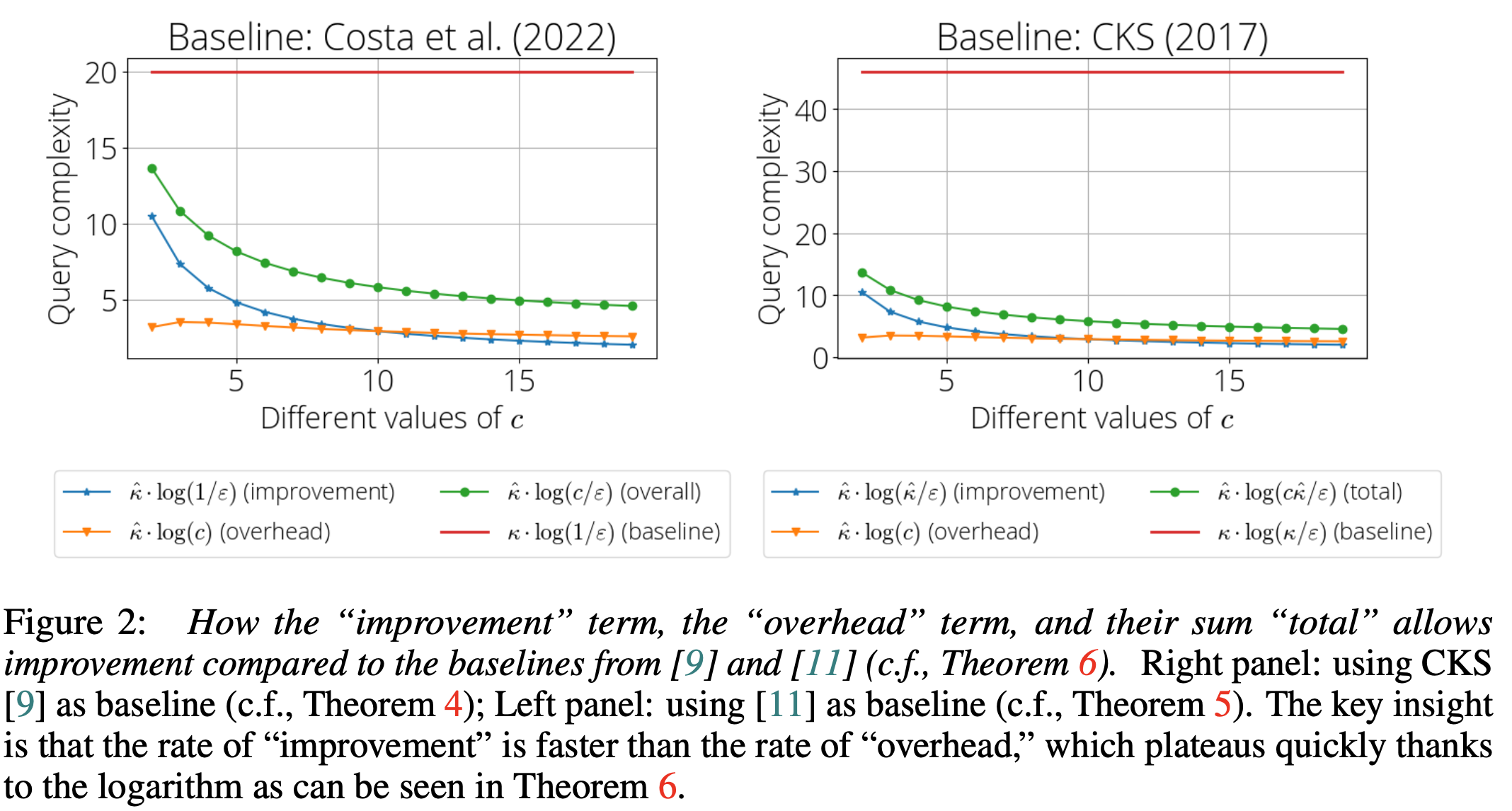
In Figure 2, we show, based on our theoretical analysis, the breakdown of the “improvement” and the “overhead” for two different QLSP solvers as subroutines.
Our proposed framework significantly alleviates the dependency on the condition number in solving the Quantum Linear System Problem (QLSP). By leveraging the proximal point algorithm (PPA), we introduce a meta-algorithm that enhances the performance of existing quantum solvers, broadening their applicability to more challenging, ill-conditioned problems.
Future work will explore several promising directions:
Our work opens new avenues for research in quantum computing and optimization, providing a robust foundation for developing more advanced algorithms that can tackle a wider range of problems.
This work is supported by NSF CMMI no. 2037545, NSF CAREER award no. 2145629, Welch Foundation Grant #A22-0307, a Microsoft Research Award, an Amazon Research Award, and a Ken Kennedy Aspiring Cluster Research award (Rice K2I).