Computing excited states of quantum systems is computationally challenging for large systems, yet quantum computing methods offer tractable scaling solutions. This problem is equivalent to Principal Component Analysis (PCA) where we're interested in decomposing a matrix into its principal components. While PCA is well-studied classically, we present Quantum EigenGame, a game-theoretic approach for finding eigenvectors where each eigenvector reaches a Nash equilibrium. By extending the classical EigenGame algorithm for quantum computers, we demonstrate convergence to excited states without requiring deflation steps. Our approach harnesses quantum computing frameworks and develops theory on error accumulation for finite-differences and parameterized approaches. Results show that Quantum EigenGame converges to excited states efficiently and accurately compared to baseline methods.

Quantum computing offers potential advantages for solving complex computational tasks, particularly for eigenvalue problems. The Variational Quantum Eigensolver (VQE) is the quantum analog of Principal Component Analysis (PCA) that approximates eigenvalue/eigenvector pairs of a given matrix (Hamiltonian). VQE can provide exponential time and space reduction over classical methods, making it crucial for finding ground state energies of molecules in quantum chemistry and materials science.

While VQE is typically used for calculating the ground state energy of a Hamiltonian, computing excited states provides broader insights into quantum systems. In chemistry, excited states help understand reaction mechanisms and absorption spectra. In materials science, they reveal information about electronic properties like conductivity and magnetism. However, calculating these higher energy states poses greater technical challenges, particularly maintaining orthogonality among calculated states.

Traditional approaches to computing excited states rely on deflation techniques, where once a ground state is found, the Hamiltonian is modified to "live" on the subspace orthogonal to this component. This process is then repeated to find subsequent excited states. While effective, deflation introduces computational burdens, especially in quantum settings where reconstructing a deflated Hamiltonian requires constructing sums of Pauli operators.

In the VQE framework, we parameterize quantum states and explore the state space through: \(|\psi(\theta)\rangle = \prod_{i=0}^{\ell-1} U_i(\theta_i)| \psi_0 \rangle\) where \(|\psi(\theta)\rangle\) is a quantum state parameterized by variables \(\theta\), and \(U_i(\theta_i)\) represents a layer of an ansatz, repeated \(\ell\) times. The goal is to optimize these parameters to find states that minimize or maximize the expectation value of the Hamiltonian.

Existing literature on excited states often uses implicit deflation algorithms that change the VQE objective to favor orthogonal solutions. Our work explores a novel approach based on game theory that exploits implicit deflation in a different way.

We present Quantum EigenGame, a novel approach to finding excited states that offers several advantages:

• Deflation-Free Algorithm: Our method computes excited states without requiring explicit deflation steps, leading to more efficient computations.
• Game-Theoretic Formulation: By posing eigenvalue calculation as a competitive game, we enable "players" to find distinct eigenvectors simultaneously or sequentially.
• Theoretical Guarantees: We provide rigorous convergence proofs for both classical 0th-order EigenGame and parameterized Quantum EigenGame, establishing robust error bounds.
• Quantum Implementation: We develop efficient quantum circuits to compute the required expectation values using minimal additional quantum resources.

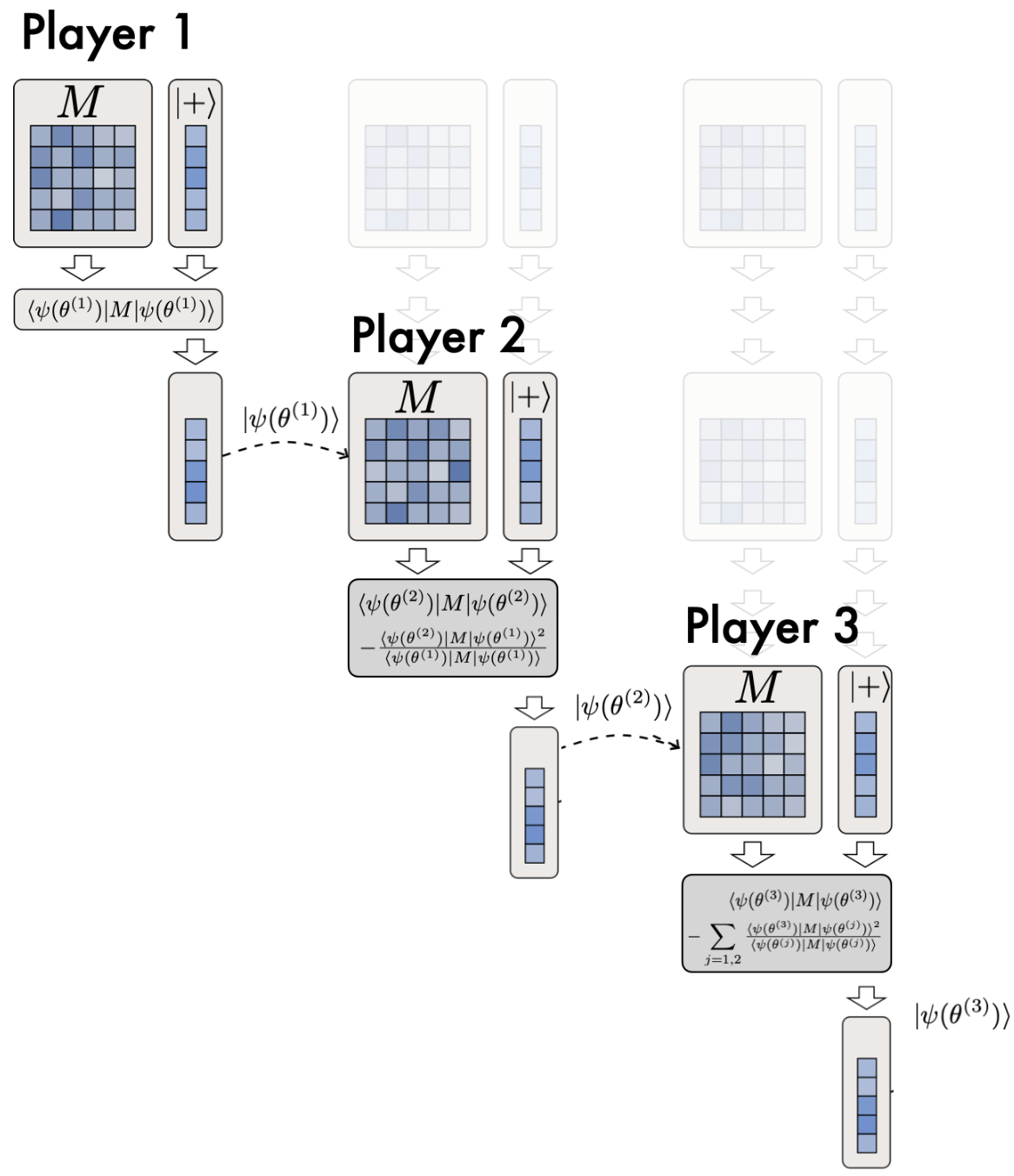
Our approach stands out by reformulating the objective function for each "player" (eigenvector) to naturally favor orthogonality to previously found states while still maximizing the variance captured. This game-theoretic perspective transforms the problem from a passive eigenvalue decomposition into an active, competitive process.

The core of our approach is the EigenGame utility function that the \(r\)-th "player" seeks to maximize:

\( \textcolor{blue}{\langle\psi(\theta^{(r)})|M|\psi(\theta^{(r)})\rangle} - \textcolor{red}{\sum_{j \le r} \tfrac{\langle \psi(\theta^{(r)})| M |\psi(\theta^{(j)})\rangle^2}{\langle \psi(\theta^{(j)})| M |\psi(\theta^{(j)})\rangle}} \)

The \(\textcolor{blue}{\text{blue}}\) term maximizes the variance along the vector being optimized, while the \(\textcolor{red}{\text{red}}\) term penalizes alignment with previously optimized vectors, ensuring orthogonality implicitly.

To implement this in a quantum setting, we developed a method to compute terms of the form \(\langle \psi(\theta^{(r)})| M |\psi(\theta^{(j)})\rangle\) using interference between quantum states. Our implementation requires only one additional qubit and two quantum oracle calls, making it efficient for near-term quantum devices.

Our theoretical analysis establishes convergence guarantees for both the 0th-order classical EigenGame (using finite differences) and the parameterized Quantum EigenGame. We also analyze error accumulation rates, showing that both methods are robust to small errors in parent eigenvectors, with error proportional to \(\mathcal{O}(\epsilon)\) for the 0th-order case and \(\mathcal{O}(\epsilon \sqrt{\ell q})\) for the parameterized case (where \(\ell\) is the number of layers and \(q\) is the number of qubits).

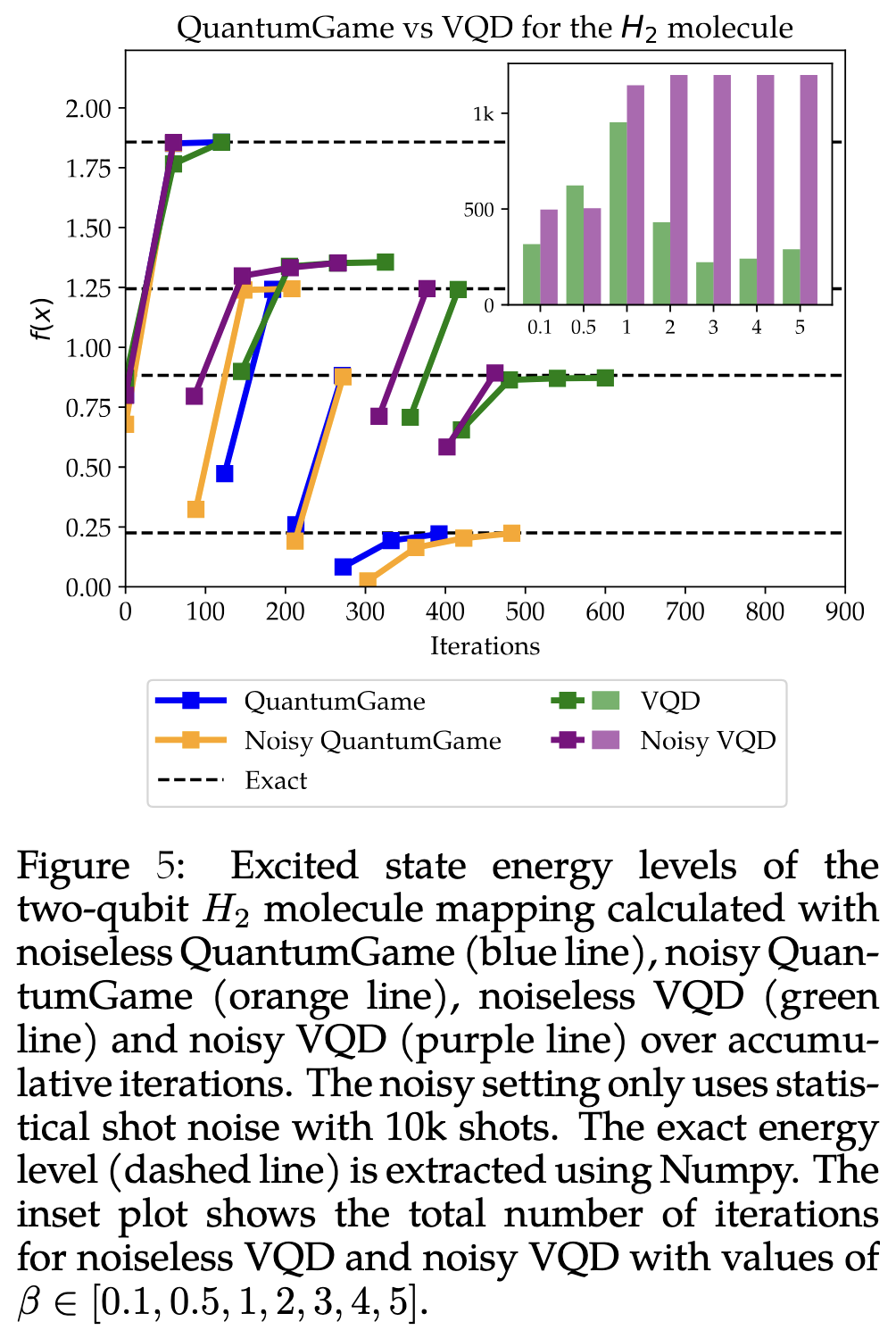
Our experiments focused on characterizing the energy levels of the H₂ molecule. We compared our Quantum EigenGame approach with the Variational Quantum Deflation (VQD) algorithm, both in noiseless and noisy settings. VQD aims to optimize a similar objective but requires a regularization parameter \(\beta\) that needs careful tuning.

Results show that Quantum EigenGame achieves comparable or better convergence rates and accuracy than VQD, especially without requiring extensive hyperparameter tuning. This makes our approach more practical for real quantum computing applications. Even in the presence of statistical shot noise (a major source of errors in quantum computation), our method maintains robust performance.

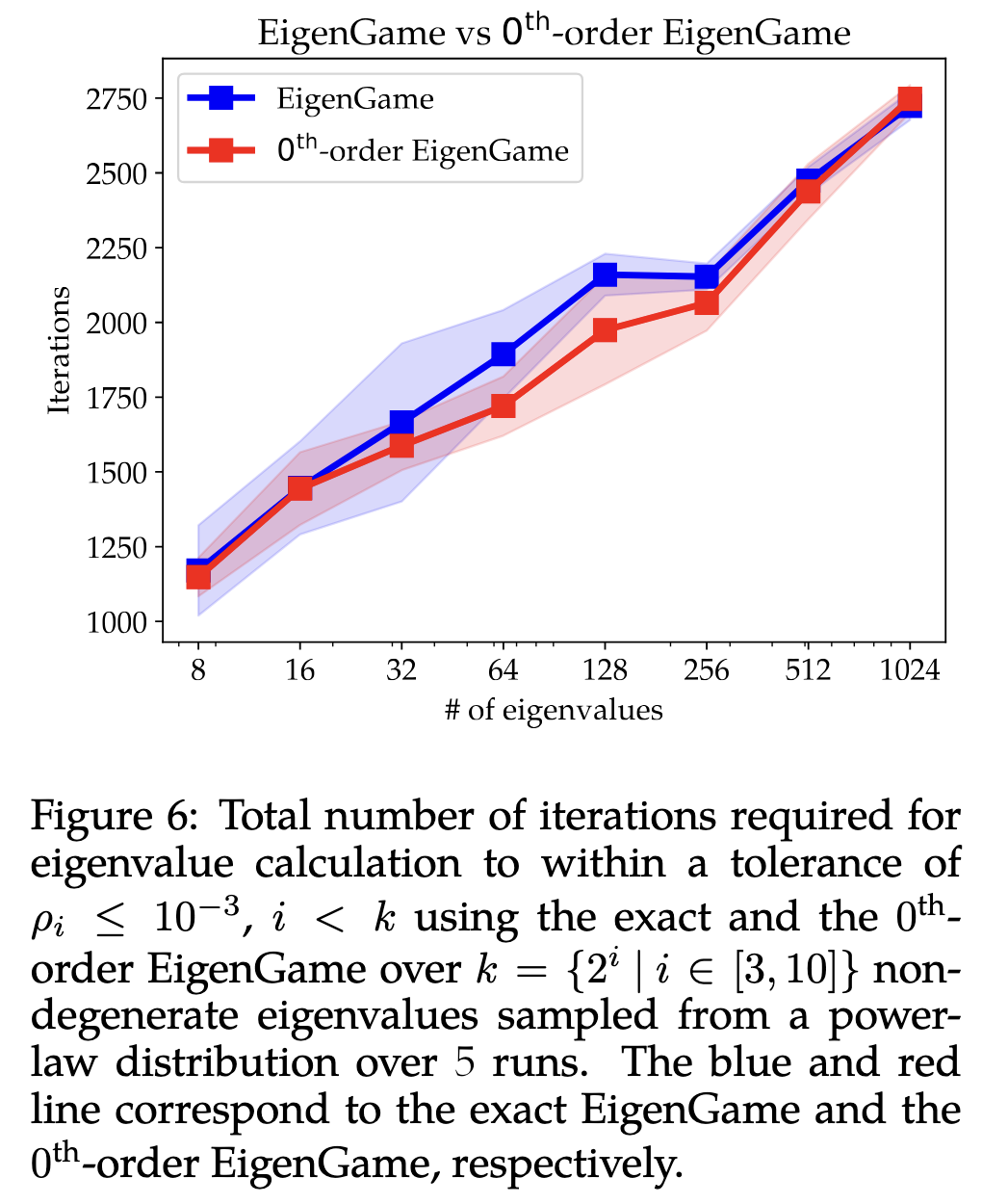
We also conducted ablation studies on the 0th-order EigenGame, comparing the number of iterations required to accurately estimate eigenvalues against the exact EigenGame across different dimensionalities. The similar scaling trend observed suggests that despite numerical errors being introduced, correct eigenvalues can still be found efficiently.

Our Quantum EigenGame approach offers a promising alternative for excited state calculations on quantum computers. By leveraging game theory principles, we avoid the computational burden of deflation steps while maintaining accuracy and improving convergence. The algorithm shows robust performance even in the presence of noise, making it suitable for NISQ-era quantum devices.

Future work will explore several promising directions:

• Parallel Implementation: Developing methods to calculate eigenvalues on different quantum devices simultaneously could further enhance efficiency.
• Theoretical Refinements: Removing unnecessary assumptions in our analysis would strengthen the theoretical foundations of our approach.
• Hardware Implementation: Testing our methods on actual quantum hardware to validate their practical utility and resilience to real-world noise.

Our work opens new avenues for quantum algorithm design, particularly for eigenvalue problems, and demonstrates how concepts from game theory can be effectively translated to the quantum domain. The results suggest that this approach could be valuable for practical quantum chemistry and materials science applications.