This blog post is about my recent work on quantum process tomography using non-convex programming. Our manuscript is on arXiv. This work has won the best student poster award at 2023 IEEE International Conference on Rebooting Computing (ICRC). This is a joint work with my student David Quiroga at Rice University.

Using Non-Convex Optimization in Quantum Process Tomography: Factored Gradient Descent is Tough to Beat

In the rapidly evolving field of quantum computing, accurately benchmarking quantum systems is paramount. Quantum Process Tomography (QPT) serves as a cornerstone for validating the operations of quantum gates and circuits, a vital step for the advancement of reliable quantum technologies. This blog post delves into a novel non-convex optimization approach for QPT, utilizing Burer-Monteiro (BM) factorization to estimate low-rank process matrices \(\chi\) for near-unitary quantum gates. Our method promises substantial computational efficiencies and robustness against noise, addressing key challenges in traditional QPT methods.

Quantum Process Tomography: A Primer

QPT aims to characterize the behavior of quantum processes, which are typically represented by completely positive and trace-preserving (CPTP) maps. These maps describe the evolution of quantum states and are crucial for implementing quantum algorithms and simulations accurately. The standard representation of a quantum process involves a density matrix \(\rho\), which evolves under these maps. The complexity of QPT lies in reconstructing the process matrix \(\chi\), which governs this evolution.

Factored Gradient Descent Approach

Our proposed method, Factored Gradient Descent (FGD), introduces a non-convex optimization framework that leverages the inherent low-rank structure of the process matrix \(\chi\). This approach significantly simplifies the landscape of the optimization problem, potentially leading to faster convergence and reduced computational requirements.

From Quantum State to Process Tomography

Building on the success of FGD in Quantum State Tomography (QST), where the state matrix $\rho$ is characterized, we extend this approach to handle the more complex process matrix \(\chi\). This extension is non-trivial, as it involves additional constraints specific to quantum processes, such as ensuring the complete positivity and trace preservation of the map.

Technical Implementation

In QPT, the process matrix \(\chi\) is reconstructed by optimizing a cost function that measures the fidelity between the predicted and actual outcomes of quantum processes. The non-convex nature of our approach comes from the factorization \(\chi = UU^\dagger\), where \(U\) is a lower-dimensional representation of \(\chi\). This factorization inherently respects the positive semi-definiteness of \(\chi\), a key requirement for physical validity.

Experimental Insights and Results

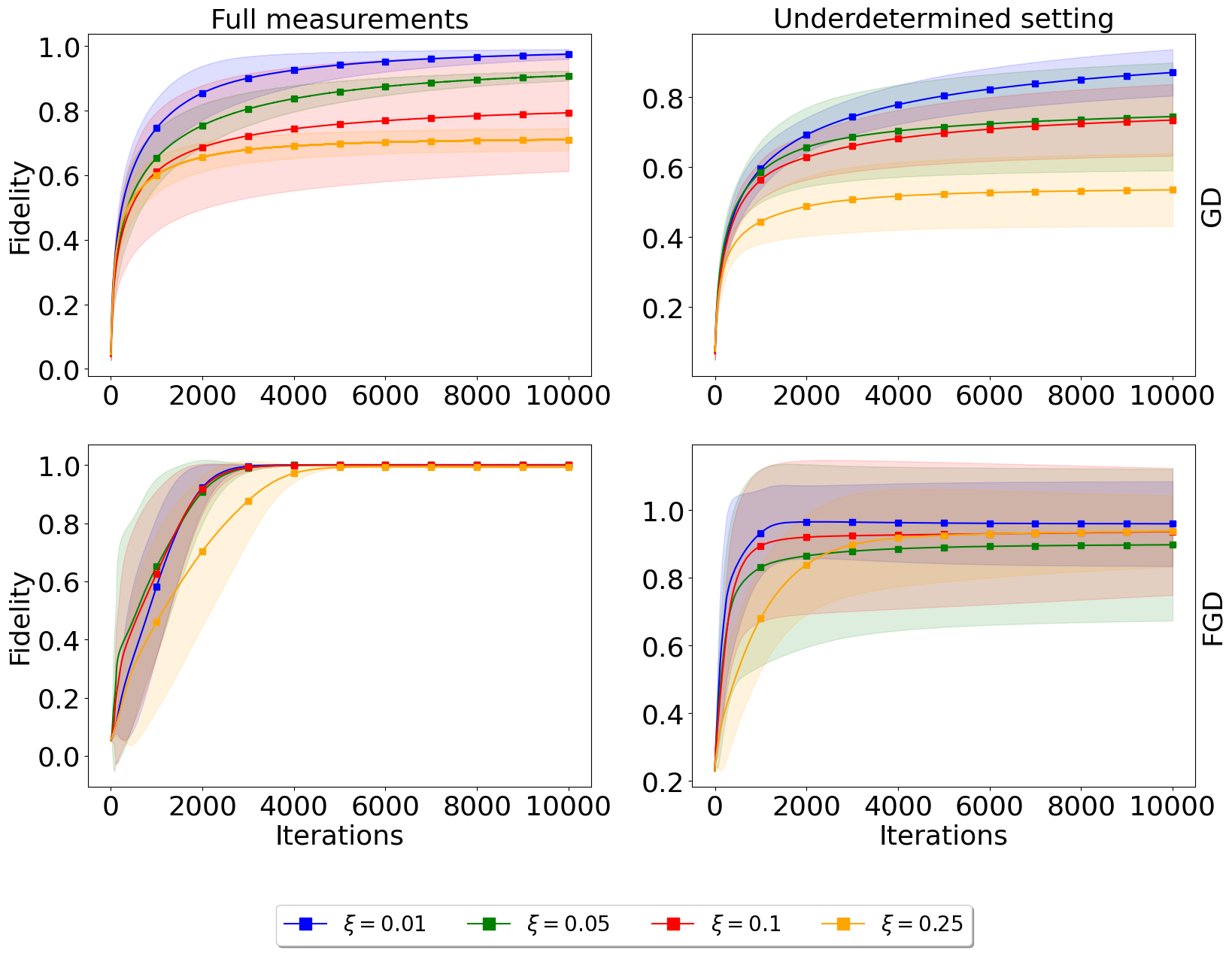
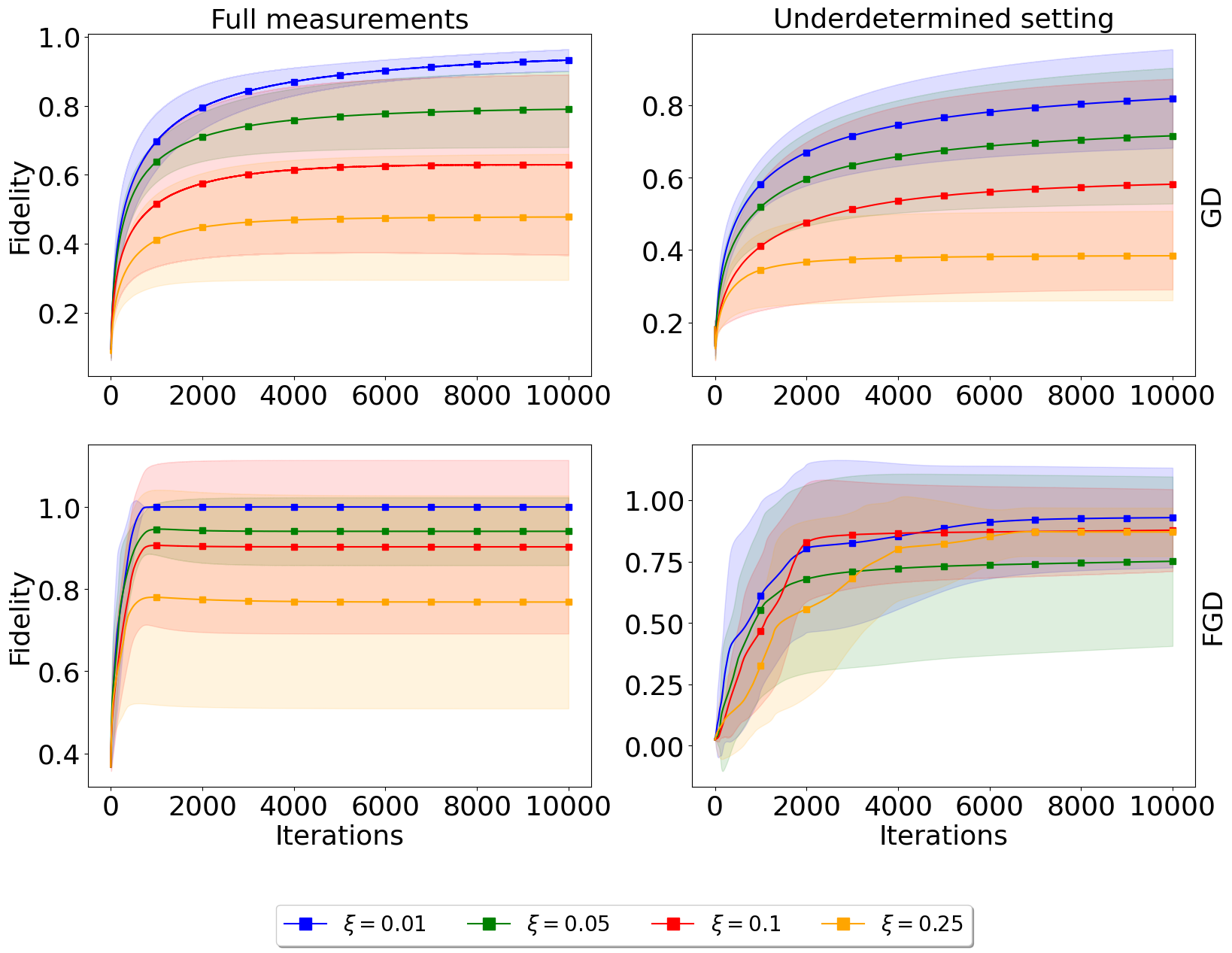
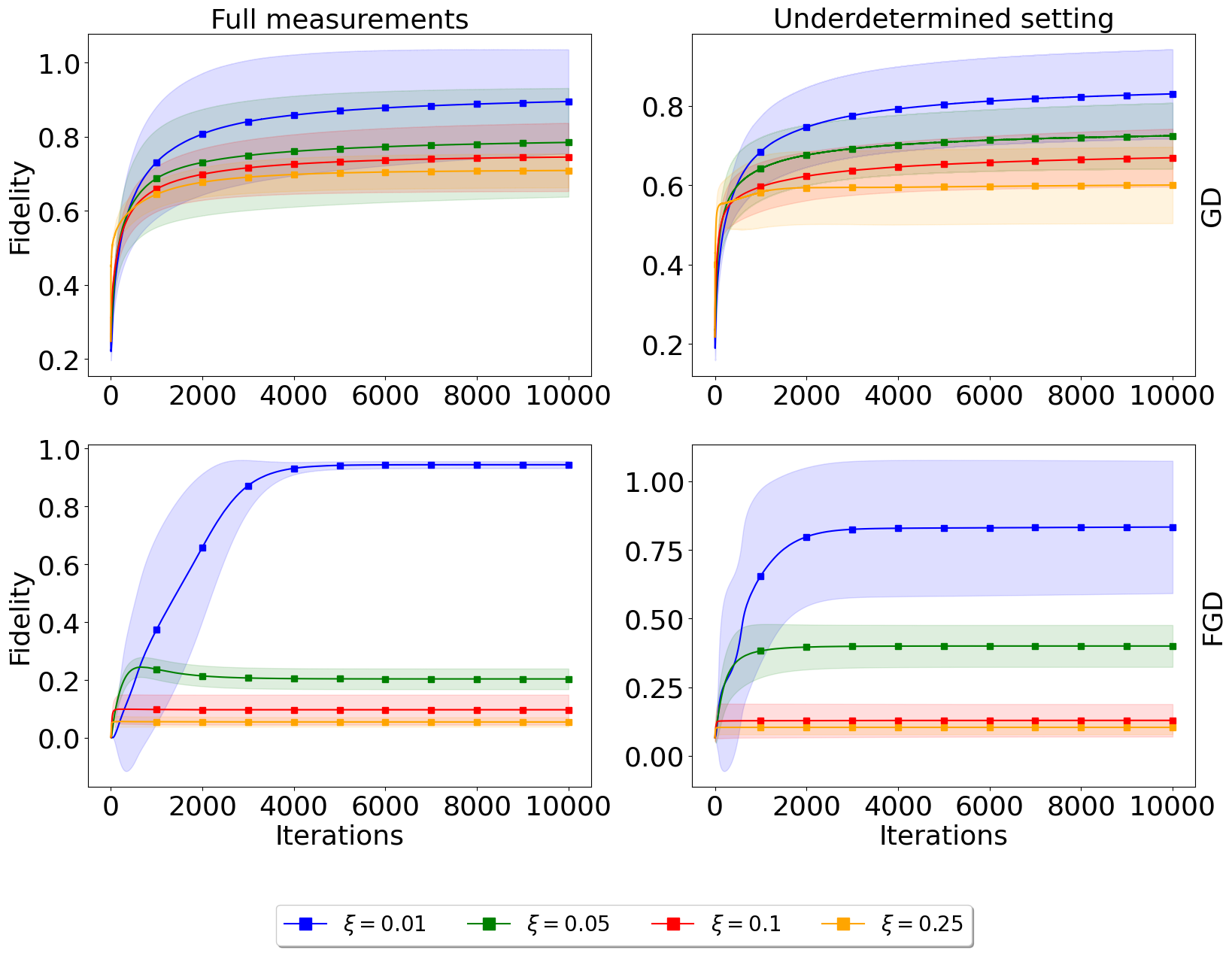
We conducted extensive simulations to compare the performance of FGD against conventional convex optimization methods under various noise models. The resilience of FGD to noise and its ability to achieve high fidelities in the reconstruction of \(\chi\) were key focus areas.

Setup and Methodology

Our experiments utilized synthetic data generated to mimic realistic quantum operations, with noise models including Gaussian and depolarizing noise. The initial states and measurement operators were carefully chosen to ensure comprehensive coverage of the process space.

Findings

The results indicate that FGD not only converges faster but also achieves higher fidelity in the reconstructed process matrices compared to traditional methods. These findings suggest that non-convex optimization could be a powerful tool in the arsenal for quantum process characterization.

Conclusions and Future Directions

The introduction of non-convex optimization techniques such as FGD into the realm of Quantum Process Tomography marks a significant advancement in the field. By addressing the computational complexities and enhancing noise resilience, FGD sets a new standard for the efficiency and accuracy of quantum process characterization.

Future work will explore theoretical bounds for the convergence and stability of FGD in QPT, alongside experimental validation on physical quantum systems. Additionally, further reduction in computational overhead and the exploration of adaptive methods for dynamic quantum systems represent exciting avenues for research.

In conclusion, the integration of sophisticated mathematical techniques such as non-convex optimization into quantum technology development is not just promising—it is imperative for the next leaps in quantum computing.

References

1. Chuang, I. L., & Nielsen, M. A. (1997). Prescription for experimental determination of the dynamics of a quantum black box. Journal of Modern Optics, 44(11-12), 2455-2467.
2. Mohseni, M., et al. (2008). Quantum process tomography for quantum information science. Quantum Information Processing, 8(4), 385-431.
3. Burer, S., & Monteiro, R. D. C. (2003). A nonlinear programming algorithm for solving semidefinite programs via low-rank factorization. Mathematical Programming, 95(2), 329-357.
4. Kyrillidis, A., et al. (2017). Provable fixed-rank approximation of a positive-semidefinite matrix from a few entries. arXiv preprint arXiv:1710.04815.