Overparameterized neural networks have led to both unexpected empirical success in deep learning, and new
techniques in analyzing neural network training. While
theoretical work in this field has led to a diverse set of new overparameterized neural network architectures and training algorithms, most efforts fall under the
following scenario: in each iteration, we perform a gradient-based update that involves all parameters of the
neural network in both the forward and backward propagation. Yet, advances in regularization techniques, computationally-efficient
and communication-efficient distributed training methods favor a different narrative: one would –explicitly or implicitly– train smaller
and randomly-selected models within a large model, iteratively. This brings up the following question:
“Can one meaningfully train an overparameterized ML model by iteratively training
and combining together smaller versions of it?”
Motivation and connection to existing methods.
The study of partial models/subnetworks that reside in a large dense network have drawn increasing attention.
- Dropout regularization. Dropout is a widely-accepted technique against overfitting in deep learning. In each training
step, a random mask is generated from some pre-defined distribution, and used to mask-out part of the
neurons in the neural network. Later variants of dropout include the drop-connect, multisample dropout , Gaussian dropout , and the variational dropout. Here, we restrict our attention to the vanilla dropout, and the multi-sample dropout.
The vanilla dropout corresponds to our framework, if in the latter we sample only one mask per iteration,
and let the subnetwork perform only one gradient descent update. The multi-sample dropout extends the
vanilla dropout in that it samples multiple masks per iteration. For regression tasks, our theoretical result
implies convergence guarantees for these two scenarios on a single hidden-layer perceptron.
- Distributed ML training. Recent advances in distributed model/parallel training have led to variants of
distributed gradient descent protocols. Yet, all training parameters are updated per outer step, which could be computationally
and communication inefficient, especially in cases of high communication costs per round. The Independent
Subnetwork Training (IST) protocol goes one step further: IST splits the model vertically,
where each machine contains all layers of the neural network, but only with a (non-overlapping) subset of
neurons being active in each layer. Multiple local SGD steps can be performed without the workers having
to communicate. Methods in this line of work achieves higher communication efficiency and accuracy that is
comparable to centralized training. Yet, the theoretical
understanding of IST is currently missing. Our theoretical result implies convergence guarantees for IST for
a single hidden-layer perceptron under the simplified assumption that every worker has full data access, and
provides insights on how the number of compute nodes affects the performance of the overall protocol.
Contributions.This paper has the following key contributions:
- We provide convergence rate guarantees for i) dropout regularization, ii) multisample dropout, iii) and multi-worker IST, given a regression task on a single-hidden layer perceptron.
- We show that the NTK of surrogate models stays close to the infinite width NTK, thus being positive definite. Consequently, our work shows that training over surrogate models still enjoys linear convergence.
- For subnetworks defined by Bernoulli masks with a fixed distribution parameter, we show that aggregated gradient in the first local step is a biased estimator of the desirable gradient of the whole network, with the bias term decreasing as the number of subnetworks grows. Moreover, all aggregated gradients during local training stays close to the aggregated gradient of the first local step. This finding leads to linear convergence of the above training framework with an error term under Bernoulli masks.
- For masks sampled from categorical distribution, we provide tight bounds i) on the average loss increase, when sampling a subnetwork from the whole network; ii) on the loss decrease, when the independently trained subnetworks are combined into the whole model. This finding leads to linear convergence with a slightly different error term than the Bernoulli mask scenario.
Main statement (informal). The following consitutes an informal statement out of this work; more details and results can be found in the extended version of the paper.
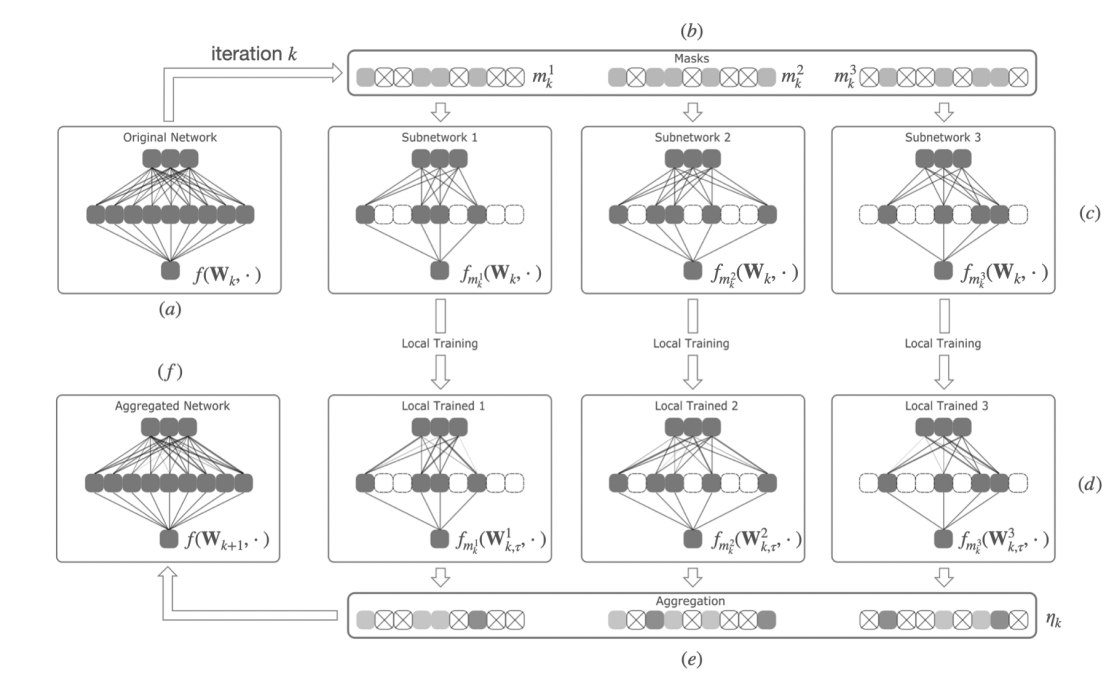
Consider the training scheme shown in Figure above. If the masks are generated from a Bernoulli distribution or categorical distribution, under
sufficiently large over-parameterization coefficient, and sufficiently small learning rate, training the large
model via surrogate subnetworks still converges linearly, up to an neighborhood around the optimal point.
|