Introduction to quantum computing: The notion of entanglement.

Sources:

“Quantum computing for computer scientists”, N. Yanofsky and M. Mannucci, Cambridge Press, 2008.

This is part of a (probably) long list of posts regarding quantum computing. In this post, we will talk about entanglement and entangled states.

Disclaimer I: while the material below might seem too simple for some scientists, I suggest not skimming over this post - personally, I always enjoy reading something that I believe I own, as επαναληψη μητηρ πασης μαθησεως (repetition is the mother of any knowledge)

Assembling systems from simpler ones

Our discussion so far has been mostly restricted to the case of a single particle. E.g., in the previous post, we discussed the case of a particle that “lies” in one of $n$ different states on a straight line.

We can use this simple case to assembly and model multiparticle quantum systems. As an instance, consider the case of particles over a line: instead of just one particle, we have two, according to the following picture:

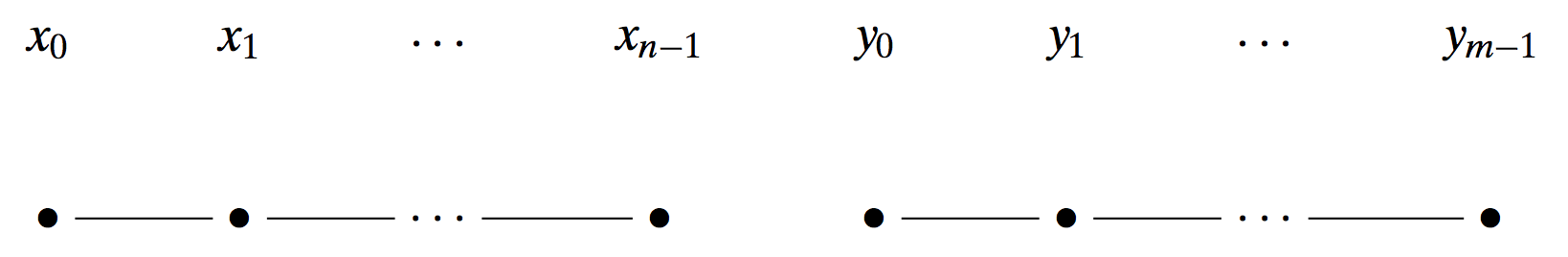
The points in the left figure can be occupied by the first particle, the points on the right figure can be occupied by the second particle. Assuming we have the basic states $ \mathcal{X} \equiv { \mathbf{x}_0, \mathbf{x}_1, \dots, \mathbf{x}_n } $ and $ \mathcal{Y} \equiv { \mathbf{y}_0, \mathbf{y}_1, \dots, \mathbf{y}_m } $ we can create the assembly of states by using the tensor product symbol $\mathcal{X} \otimes \mathcal{Y}$, where the possible states are:

\[| \mathbf{x}_0 \rangle \otimes | \mathbf{y}_0 \rangle \\ | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_1 \rangle \\ \vdots \\ | \mathbf{x}_1 \rangle \otimes | \mathbf{y}_0 \rangle \\ \vdots \\ | \mathbf{x}_{n-1} \rangle \otimes | \mathbf{y}_{m-1} \rangle.\]

Ηere, $| \mathbf{x}_i \rangle \otimes | \mathbf{y}_j \rangle $ means that the first particle is in state $i$ of $\mathcal{X}$ and the second particle is in state $j$ of $\mathcal{Y}$.

Using all possible combinations, we can write down the state of two particles as a superposition of basic states such as:

\[| \mathbf{\psi} \rangle = c_{0, 0} \cdot | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_0 \rangle + \cdots + c_{n-1, m-1} \cdot | \mathbf{x}_{n-1} \rangle \otimes | \mathbf{y}_{m-1} \rangle.\]

As an example, consider $n = m = 2$ and assume that we can describe the state $| \mathbf{\psi} \rangle$ as:

\[| \mathbf{\psi} \rangle = i \cdot | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_0 \rangle + (1-i) \cdot | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_1 \rangle + 2 \cdot | \mathbf{x}_1 \rangle \otimes | \mathbf{y}_0 \rangle + (-1 -i) \cdot | \mathbf{x}_1 \rangle \otimes | \mathbf{y}_1 \rangle.\]

Then, we can compute the probability of being at the state $| \mathbf{x}_1 \rangle \otimes | \mathbf{y}_1 \rangle$ as:

\[\mathbb{P}[| \mathbf{x}_1 \rangle \otimes | \mathbf{y}_1 \rangle] = \frac{| -1 - i|^2}{|i|^2 + |1 - i|^2 + |2|^2 + |-1 - i|^2} = 0.2222.\]

Entanglement

The discussion so far indicates that the state of an assembly of simpler quantum systems can be described as the tensor product of the states of each individual system. I.e., we can describe the overall system by looking into the constituents. However, this is not always true for quantum systems. Here, we will just describe this via an example.

Assume the simple case above where $n = m = 2$. And assume that the current state $| \mathbf{\psi} \rangle$ satisfies:

\[| \mathbf{\psi} \rangle = | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_0 \rangle + | \mathbf{x}_1 \rangle \otimes | \mathbf{y}_1 \rangle \\ = 1 \cdot | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_0 \rangle + 0 \cdot | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_1 \rangle + 0 \cdot | \mathbf{x}_1 \rangle \otimes | \mathbf{y}_0 \rangle + 1 \cdot | \mathbf{x}_1 \rangle \otimes | \mathbf{y}_1 \rangle.\]

Let us see whether we can describe the above state as the tensor product of the basic states of single particles. Remember that the state using only the first particle can be described as:

\[c_0 \cdot |\mathbf{x}_0 \rangle + c_1 \cdot | \mathbf{x}_1 \rangle,\]

and the state using only the second particle can be described as:

\[c_0' \cdot |\mathbf{y}_0 \rangle + c_1' \cdot |\mathbf{y}_1 \rangle.\]

Let us “create” the states of the two particle system by assembling the simple systems: i.e., we compute the tensor product of their states. In particular, we have:

\[\left( c_0 \cdot |\mathbf{x}_0 \rangle + c_1 \cdot | \mathbf{x}_1 \rangle \right) \otimes \left( c_0' \cdot |\mathbf{y}_0 \rangle + c_1' \cdot |\mathbf{y}_1 \rangle\right) = \\ c_0 c_0' \cdot | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_0 \rangle + c_0 c_1' \cdot | \mathbf{x}_0 \rangle \otimes | \mathbf{y}_1 \rangle + c_1 c_0' \cdot | \mathbf{x}_1 \rangle \otimes | \mathbf{y}_0 \rangle + c_1 c_1' \cdot | \mathbf{x}_1 \rangle \otimes | \mathbf{y}_1 \rangle.\]

We need to choose the coefficients in order to create $| \mathbf{\psi} \rangle$. However, this means that $c_0 c_0’ = c_1 c_1’ = 1$ and $c_0 c_1’ = c_1 c_0’ = 0$. These two equations have no solution: we cannot use the basic states and the tensor product to generate the state. In this case, we say that the two particles are entangled.

To see what it means in practice, let us consider the following: Assume we measure the first particle and we find it in position $\mathbf{x}_0$. Can we use this information to infer the state of the other particle? Yes! We can see that the component $|\mathbf{x}_0 \rangle \otimes | \mathbf{y}_1 \rangle$ has coefficient 0 in the expression of the state of the two particles. This means that, if we found first particle in $\mathbf{x}_0$, we will find the second particle in state $\mathbf{y}_0$. The surprising fact is that the two particles could be light years away and we can still infer the state of the individual particles by observing one of them!

To wrap it up: if we can infer some information of some particles by looking some others, we say that the particles are entangled. If this is not the case, then the particles are separable.

How is entanglement used

We will leave this story short: we will just mention that entanglement is used in algorithms, in cryptography and in teleportation. We will discuss (at least a subset of) these in the posts to follow. Stay tuned!